＜問題＞
図１のように，矢印の向きに順番にご石をならべていく。このとき図２のように，ご石の
中心と中心を結んでできる正三角形(かげのついた部分のような正三角形)の面積は，いず
れも１m2となる。
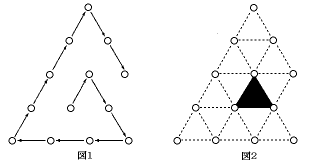
ならべるご石の数と，できる正三角形の面積の合計との関係を考える。例えば，図２のよ
うに１３個のご石をならべると，その正三角形の面積の合計は１３m2になる。
次の文章の
にあてはまる数を答えなさい。(1) ２０個のご石をならべると，正三角形の面積の合計は
m2である。(2)
個のご石をならべると，正三角形の面積の合計は１９５m2である。(3) ５００個のご石をならべると，正三角形の面積の合計は
m2である。＜解答＞
(1) まず、ご石全部で完全な正三角形ができる場合を考えます。
できる小さな正三角形の面積の合計は辺の長さの２乗に比例して増えます。
| １辺の長さ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ・・・ |
| ご石の個数 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 56 | 68 | ・・・ |
| 面積 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | ・・・ |
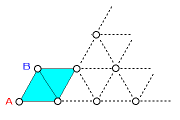
表の状態から次に１個（図のＡ）を増やしても、正三角形の個数は変わりません。
また、その次の１個（図のＢ）を増やすと、青い正三角形２個増えます。以下、しば
らくの間、ご石を１個増やすごとに小さな正三角形が２個ずつ増え続けます。
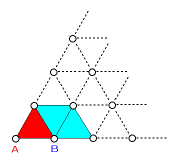
表の状態から最後に増やした１個（図のＡ）を減らすと、赤い正三角形１個が減りま
す。また、その前の１個（図のＢ）を減らすと、青い正三角形２個減ります。以下、
しばらくの間、ご石を１個減らすごとに小さな正三角形が２個ずつ減り続けます。
ご石を２０個並べる場合は、完全な正三角形になる２１個より小さな正三角形が１個
だけ少ない。
２５−１＝２４
２４個の小さな正三角形ができるので、面積は２４m2です。
答 ２４m2
(2) １９５より大きくて最も近い平方数を考えます。
１３×１３＝１６９、１４×１４＝１９６
１辺の長さが１４となる時の個数より小さな正三角形が１個少ないことがわかります
１辺の長さが１４になるのは１辺のご石が１５の時で、その時のご石の個数は、
（１＋１５）×１５÷２＝１２０個
１２０−１＝１１９個
答 １１９個
(3) １辺に並べたご石の個数をもとにご石の個数を考えます。
（１＋１５）×１５÷２＝１２０
（１＋２０）×２０÷２＝２１０
（１＋２５）×２５÷２＝３２５
（１＋３０）×３０÷２＝４６５
（１＋３１）×３１÷２＝４９６
ご石が１辺に３１個ならんでいる場合は辺の長さは３０で、小さな正三角形の面積の
合計は、
３０×３０＝９００m2
あと４個増やすとご石は５００個になります。
この時増える小さな正三角形は全部で、
０＋２＋２＋２＝６個
よって、面積の合計は、
９００m2＋６m2＝９０６m2
答 ９０６m2