<問題>
下の図は,ある立体を(真上から見た図),(真正面から見た図),(左側から見た図)です。
これらの図は直角三角形,長方形,半円でできています。次の問に答えなさい。
ただし,図の数値の単位はcmとし,円周率は3.14とします。
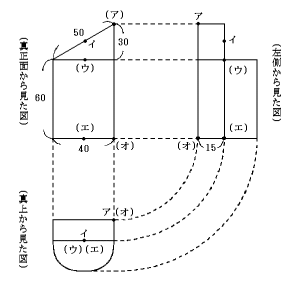
*図の(ア)のような( )付の点は手前に点や辺があって,見えないという意味です。
また,(真正面から見た図)中の点イ,(ウ),(エ)はそれぞれ辺の真ん中の点です。
(1) この立体の体積は何cm3ですか。
(2) この立体を点ア,イ,ウ,エ,オを通る平面で切ったときの切り口の面積は何cm2で
すか。
<解答>
(1) この立体は半円柱、直方体、三角柱を組み合わせた立体です。なお、直方体と三角柱
をまとめて五角柱と考えることもできます。
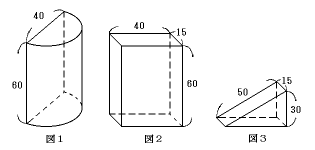
<半円柱(図1)> 底面の半径:20cm、高さ:60cm
<直方体(図2)> 縦:15cm、横40cm、高さ:60cm
<三角柱(図3)> 底面の底辺:40cm、底面の高さ:30cm
三角柱の高さ:15cm
それぞれの体積を順に求めていきます。
(20×20×3.14÷2)×60=37680cm3
15×40×60=36000cm3
(40×30÷2)×15=9000cm3
よって、求める立体の体積は、
37680+36000+9000=82680cm3
答 82680cm3
(2) 五角柱の部分の切り口と半円柱の部分の切り口を別々に考えます。
上から見ると次の図4のように切れ目が見えます。
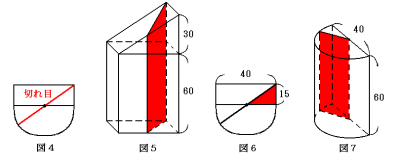
五角柱の部分では、図5のように切り口の形が台形です。
図5から、
下底:60+30=90cm
上底:60+30÷2=75cm
図6で赤い直角三角形の3辺の比が3:4:5になることを使って、
高さ:15÷3×5=25cm
切り口の台形の面積は、
(75+90)×25÷2=2062.5cm2
切れ目が2つの底面の半円の中心を通るので、半円柱の部分の切り口は長方形になり
ます。
図7から、縦は半円柱の高さ、横は半円柱の底面の半径にあたるので、
切り口の長方形の面積は、
60×20=1200cm2
切り口の面積は、
2062.5+1200=3262.5cm2
答 3262.5cm2