<問題>
次の図で四角形ABCDは1辺の長さが5cmのひし形,AE=3cm,EB=4cmです。
四角形ABCDを直線Lを軸として1回転させたときにできる立体について,次の問
に答えなさい。ただし,円周率は3.14とします。
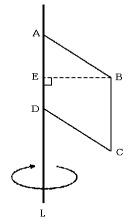
(1) 立体の体積を求めなさい。
(2) 立体の表面積を求めなさい。
<解答>
回転体の体積は、次のように2種の立体をもとに分けて考えることができます。
A:回転軸に接する平行四辺形でできる立体
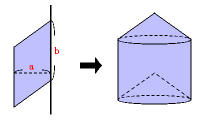
円柱の体積と同じ計算になり、
体積=(a×a×3.14)×b=a×a×b×3.14
B:回転軸に接する三角形でできる立体
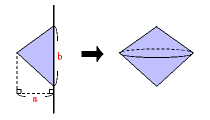
円錐の体積と同じ計算になり、
体積=(a×a×3.14)×b÷3=a×a×b×
回転体の表面積は、次の3種の線分でできる図形をもとに考えることができます。
A:回転軸に接し、回転軸に垂直な線分でできる図形
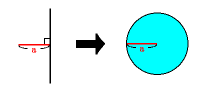
円になるので、
面積=a×a×3.14<
B:回転軸に接し、回転軸に垂直でない線分でできる図形
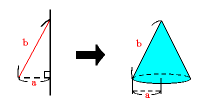
円錐の側面になるので、
面積=a×b×3.14
C:回転軸に平行な線分でできる図形
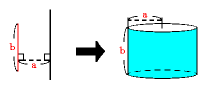
円柱の側面になるので、
面積=(a×2×3.14)×b=a×b×2×3.14
この問題では使いませんが、多くの問題では相似の性質も使って長さ・面積・体積の比
を求めて解いていきます。
(1) 回転軸に接した平行四辺形を回転させた場合なので、
4×4×5×3.14=251.2cm3
答 251.2cm3
(2) 2辺AB、DCでできる図形の面積は等しく、
4×5×3.14×2=125.6cm2
辺BCでできる図形の面積は、
4×5×2×3.14=125.6cm2
よって表面積は、
125.6+125.6=251.2cm2
答 251.2cm2