＜問題＞
次図のように色のついた部分まで水の入った立体を水平な床の上に置きます。この立体
を面ＥＦＧＨを底面として置くと水面までの高さは，この立体を逆さにして面ＡＢＣＤを
底面として置いたときの水面までの高さより２cm低くなります。
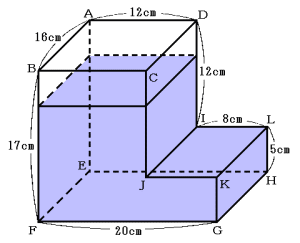
(1) 面ＥＦＧＨを底面として置いたときの水面までの高さを求めなさい。
(2) 面ＥＦＧＨを底面として置き，面ＡＢＣＤを取り外しました。
ＦＧを床につけたまま，側面ＢＦＧＫＪＣが床と45°となるように傾けたとき，流れ
出た水の量は何ｃm3ですか。
(3) (2) の後，再び面ＥＦＧＨを底面として置き，今度はＥＦを床につけたまま，側面Ａ
ＢＦＥが床と45°となるように傾けました。このときの床から水面までの高さを求め
なさい。
＜解答＞
＊容器の頂点だけを下につけて傾けた場合ではないので、手前から見える部分を底面とし
て考えて解きます。
(1) 容器で水の入っていない部分を考えます。
面ＢＦＧＫＪＣ側から見た、次の２つの図の奥行きは等しくなります。
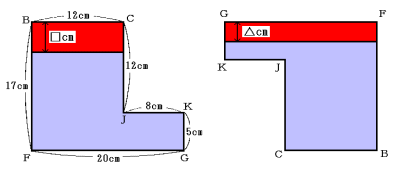
左の図の赤い長方形の面積と右の図の赤い長方形の面積は等しいので、
□：△＝
：
＝５：３□と△の差が水面の高さの差なので、
□＝２cm÷（５−３）×５＝５cm
水面の高さは、
１７cm−５cm＝１２cm
答 １２cm
(2) こちらも容器で水の入っていない部分を考えます。
４５度だけ傾けた場合には、面ＫＧＨＬ側から見た図は次の図のようになります。
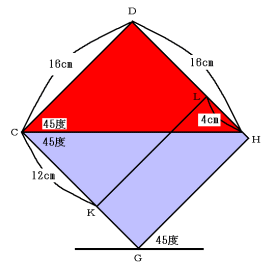
手前にできる水が入っていない部分の三角柱の体積は、
（４×４×
）×８＝６４ｃm3奥にできる直方体で水が入っていない部分の三角柱の体積は、
（１６×１６×
）×１２＝１５３６ｃm3もともと水が入っていなかった部分の体積は、
１６×１２×５＝９６０ｃm3
よって、流れ出た体積は、
（６４＋１５３６）−９６０＝６４０ｃm3
答 ６４０ｃm3
(3) こちらは容器で水の入っている部分を考えます。
水が入っている水の量は、
１６×１２×１２＋１６×２０×５−（６４＋１５３６）
＝２３０４＋１６００−１６００
＝２３０４ｃm3
よって面ＢＦＧＫＪＣ側から見た図で、水が入っている部分の面積は、
２３０４÷１５＝１４４ｃm2
まず図形が完全な直角二等辺三角形なると考えます。
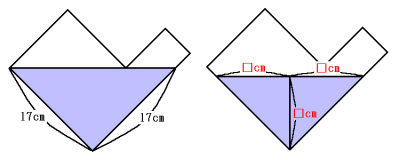
左の図のようになる場合が最大で、その面積は、
１７×１７×
＝１４４．５ｃm3これより小さいので、右の図のように深さを□cmとして計算できます。
（□×２）×□×
＝１４４□×□＝１４４
□＝１２
答 １２cm