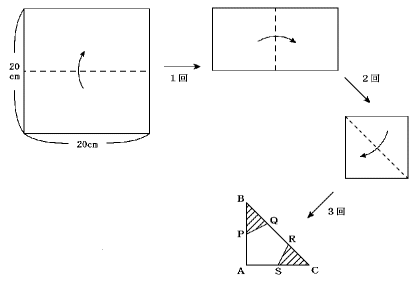
＜問題＞
１辺の長さが２０cmの正方形の紙を下の図のように３回折った後，ＰＱとＳＲ切り取り
ました。その後，もとのように広げたとき紙の面積は何ｃm3ですか。ただし，Ｐ，Ｓはそ
れぞれＡＢ，ＡＣのまん中の点，Ｑ，ＲｈａＢＣを３等分した点です。
＜解答＞
元に戻した時の形を考える場合には、折り目に関して対称であることに注目して逆に戻
しながら考えていきます。
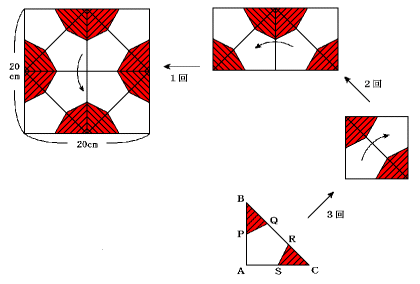
この問題では面積を考えるのでもっと簡単です。
最後にできた直角二等辺三角形はどの場所でも紙が８枚重なっているので、正方形の紙
は元は戻すと、上の図のように８個の直角二等辺三角形に分けるよう折り目が付いてい
ます。
そのため、それぞれの直角二等辺三角形で切り落とされた部分とそうでない部分の面積
の比は、正方形で切り落とされた部分とそうでない部分の面積の比と同じになります。
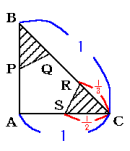
最後の直角二等辺三角形で、切り落とされた部分の割合は、
× 
×２＝よって、広げたときの紙の面積は、
２０×２０×（１−
）＝２６６
ｃm2答 ２６６
ｃm2