<問題>
A君とB君が、ある地点を10時に出発し、13.5kmはなれた地点まで歩きました。
A君は30分ごとに休けいをとって、下図のように歩きました。B君は休けいをとらずに
―定の速さで歩き、A君と同時にとう着しました。次の問に答えなさい。
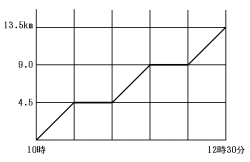
(1) A君の歩く速さは分速何mですか。
(2) B君の歩く速さは分速何mですか。
(3) B君がA君に初めて追いつくのは、何時何分ですか。
(4) A君とB君のきょりがちょうど600mになるのは、何時何分ですか。
最初の場合と最後の場合だけ答えなさい。
<解答>
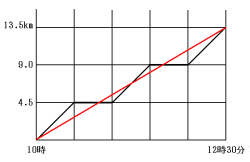
(1) グラフからA君は30分で4.5km進んだことがわかります。
4500m÷30分=分速150m
答 分速150m
(2) グラフからB君は2時間30分で13.5km進んだことがわかります。
13500m÷150分=分速90m
答 分速90m
(3) グラフからB君がA君に初めて追いついたのは、A君が4.5kmの地点で休憩してし
ている時だとわかります。
4500m÷分速90m=50分
出発後50分なので10時50分です。
答 10時50分
(4) 2人の距離は10時30分まで広がり、その後10時50分まで縮まります。
2人の速さの差を考えて、距離が600mに広がるまでの時間を求めます。
600m÷(分速150m−分速90m)=10分
最初は出発10分後の10時10分です。
2人の移動の様子を表すグラフは、ちょうど半分進んだ11時45分の時点を中心に
点対称です。
よって、
最後に2人の距離が600mになったのは到着10分前の12時20分です。
答 最初:10時10分 最後:12時20分