算数

　　　　「線分の長さと三角形の面積の比」

　　　　線分の長さの比を用いて三角形の面積比を考える問題は、高さまたは底辺が等しい場合と
　　　　相似の場合がよく出されます。この問題は両方の考え方が使われています。練習問題とし
　　　　て利用しても良いものです。

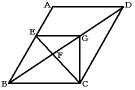
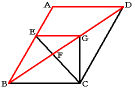
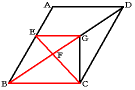
＜問題＞ 次の平行四辺形ＡＢＣＤで，ＢＥ＝３cm，ＣＤ＝５cmである。ＣＥとＢＤの交点をＦ，ＥからＢＣに平行な線をひき，ＢＤとの交点をＧとするとき，次の問いに答えよ。 　　　　 (1) ＢＦ：ＦＧ：ＧＤを求めなさい。 (2) 平行四辺形ＡＢＣＤの面積が４８ｃm2のとき，三角形ＥＧＣの面積を求めなさい。 ＜解答＞ (1) 平行四辺形の対辺は等しいので、ＢＡ＝ＣＤ＝５cm 　　ＡＤとＥＧは平行なので、２つの三角形ＡＢＤとＥＢＧは相似です。 　　　　 　　　ＢＡ：ＢＥ＝ＥＧ：ＡＤ＝ＢＧ：ＢＤ＝３：５ 　　同様に平行四辺形の対辺は等しいので、ＢＣ＝ＡＤ 　　ＢＣとＥＧは平行なので、２つの三角形ＦＢＣとＦＧＥは相似です。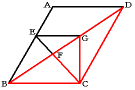 　　　　 　　　ＢＦ：ＧＦ＝ＢＣ：ＧＥ＝ＡＤ：ＥＧ＝５：３ 　　ここで、ＢＤ＝１とすると、 　　　ＢＧ＝、ＧＤ＝ 　　さらに、 　　　ＢＦ＝ＢＧ× 　　　　　＝× 　　　　　＝ 　　　ＦＧ＝ＢＧ−ＢＦ 　　　　　＝− 　　　　　＝ 　　よって、 　　　ＢＦ：ＦＧ：ＧＤ＝：： 　　　　　　　　　　　＝１５：９：１６ 　　　　　　　　　　　　　　　　　　　　　　　　　　　答　１５：９：１６ (2) 平行四辺形は対角線で面積が２等分されるので、 　　　三角形ＡＢＤ＝三角形ＢＣＤ＝４８÷２＝２４ｃm2 　　高さの等しい三角形の面積の比は底辺の比なので、 　　　　 　　　三角形ＣＢＦ：三角形ＣＦＧ：三角形ＣＧＤ＝ＢＦ：ＦＧ：ＧＤ 　　　　　　　　　　　　　　　　　　　　　　　＝１５：９：１６ 　　　三角形ＦＣＧ＝三角形ＢＣＤ× 　　　　　　　　　＝２４× 　　　　　　　　　＝５ 　　一般的な三角形の面積比は（底辺×高さ）の比なので、 　　　　 　　　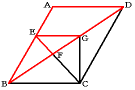三角形ＥＦＧ：三角形ＡＢＤ＝（ＦＧ×ＥＢ）：（ＢＤ×ＡＢ） 　　　　　　　　　　　　　　　　＝（９×３）：（４０×５） 　　　　　　　　　　　　　　　　＝２７：２００ 　　　三角形ＥＦＧ＝三角形ＡＢＤ× 　　　　　　　　　＝２４× 　　　　　　　　　＝３ 　　これらから、 　　　　三角形ＥＧＣ＝三角形ＦＣＧ＋三角形ＥＦＧ 　　　　　　　　　　＝５＋３< 　　　　　　　　　　＝８ 　　　　　　　　　　　　　　　　　　　　　　　　　　答　８ｃm2

ページTopへ