入試問題のポイント(算数)
■点の移動によってできる図形
動点を考える問題はある状況になるときまでにかかる時間を考える問題です。速さ・周期性・相似などの融合問題になっているのが特徴で、以前はいろいろな入試難度の学校でよく出されました。この問題も一般的な考え方を組み合わせた問題で、中堅レベルの学校の志望者は練習問題として使うと良いでしょう。
■問題
次の図のような長方形ABCDがあります。点E,Fはそれぞれ辺AB,DCのまん中の点で,点Pは,EF上を点EからFまで毎秒3cmの速さ,点Qは辺DA上を点DからAまで毎秒4cmの速さで動きます。点P,Qが同時に出発するとして,次の(1)〜(2)の問いに答えなさい。
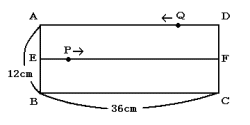
(1) 2点P,Qが出発してから6秒後の四角形ABPQの面積は何cm2ですか。
(2) 四角形ABPQが台形になるのは,2点P,Qが出発してから何秒後ですか。
(3) 3点Q,P,Cが一直線に並ぶのは,2点P,Qが出発してから何秒後ですか。
■解答
(1) 図に表すと次のようになります。
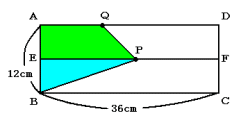
四角形ABPQは台形AEPQと直角三角形BEPに分けられるので,
AQの長さ 36cm−毎秒4cm×6秒=12cm
EPの長さ 毎秒3cm×6秒=18cm
台形AEPQの面積 (12+18)cm×6cm÷2=90cm2
直角三角形BEPの面積 18cm×6cm÷2=54cm2
これより,
90+54=144cm2
答 144cm2
(2) 図に表すと次のようになる時です。
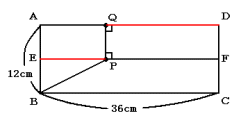
DPとEPの長さの和がADの長さと等しくなるので,
36cm÷毎秒(4+3)cm=5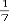 秒
秒
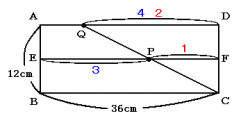
答 5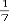 秒後
秒後
(3) 図に表すと次のようになる時です。
三角形CPFと三角形CQDとが相似になるので,
QD:PF=CD:CF=2:1
また,速さの比から,
QD:EP=4:3
この2つの比から,
EP:PF=3:2
よって,
EPの長さ 36cm×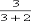 =
=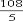 cm
cm
かかった時間 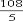 cm÷毎秒3cm=7
cm÷毎秒3cm=7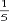 秒
秒