入試問題のポイント（算数）
■三角形の相似・合同の利用
中学入試でよく出される問題です。難度に違いはあっても、ほとんどの学校で出されます。十分に練習問題を解いて入試に臨みましょう。
■問題
次の問いに答えなさい。
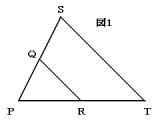
[1] 図１で，点Ｑ，ＲはそれぞれＰＳ，ＰＴの真ん中の点です。
三角形ＰＳＴの面積は三角形ＰＱＲの何倍ですか。
[2] 図２は，ＢＣの長さが２cmの直角三角形ＡＢＣで，ＢＰは角Ｂをちょうど二等分しています。
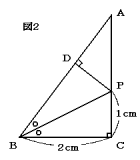
ＡＢとＰＤが垂直に交わっているとき，
(1) ＰＤの長さを求めなさい。
(2) 三角形ＰＡＢの面積を求めなさい。
(3) ＡＢとＡＰの長さを求めなさい。
■解答
[1] 三角形ＰＴＳと三角形ＰＱＲが相似であることを利用して解きます。
三角形ＰＴＳと三角形ＰＱＲの相似比は、
ＰＴ：ＰＳ＝２：１
相似形の面積比は相似比の２乗の比になるので、
（２×２）：（１×１）＝４：１
よって、三角形ＰＳＴの面積は三角形ＰＱＲの４倍です。
答 ４倍
[2] (1) 角ＰＢＣ＝角ＰＢＤ、角ＰＣＢ＝角ＰＤＢ＝９０度、辺ＰＢは共通です。
１つの辺の長さとその両端にある角の大きさの等しいので、
三角形ＰＢＣと三角形ＰＢＤは合同です。
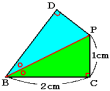
辺ＰＣと辺ＰＤは対応する辺なので、ＰＤの長さも１cmです。
答 １cm
(2) 角ＡＣＢ＝角ＡＤＰ＝９０度、また角ＢＡＣと角ＰＡＤは同じ角です。
２つの角がそれぞれ等しいので、三角形ＡＢＣと三角形ＡＰＤは相似です。
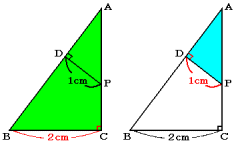
この相似比を求めると、
ＢＣ：ＰＤ＝２：１
２つの三角形の面積比は、
（２×２）：（１×１）＝４：１
ここで、三角形ＡＰＤの面積＝１とすると、
三角形ＡＢＣの面積＝４
四角形ＢＣＰＤの面積＝４−１＝３
三角形ＰＢＣの面積＝３÷２＝
と決まります。
三角形ＰＢＣの面積は、
２cm×１cm÷２＝１ｃm2
よって、
三角形ＡＰＤの面積＝１ｃm2÷＝
ｃm2
三角形ＡＢＣの面積＝ｃm2×４＝
ｃm2
三角形ＰＡＢの面積＝三角形ＡＢＣの面積−三角形ＰＢＣの面積
＝ｃm2−１ｃm2
＝
ｃm2
答 ｃm2
（１ｃm2）
(3) 三角形ＰＡＢは、
あ）底辺をＡＢとすると高さがＰＤになる。
い）底辺をＡＰとすると高さがＢＣになる。
あ）から、
ＡＢの長さ×１cm÷２＝ｃm2
ＡＢの長さ＝ｃm2×２÷１cm＝
cm
い）から、
ＡＰの長さ×２cm÷２＝ｃm2
ＡＰの長さ＝ｃm2×２÷２cm＝cm
答 ＡＢの長さ：cm（３
cm）、ＡＰの長さ：cm（１cm）