入試問題のポイント(算数)
■相似三角形の辺の長さの比と面積の比
直角三角形で相似を考える問題は平行線を使う問題とともに中学受験では一般的な相似の問題です。図を見た瞬間に相似三角形を見つけ,さらにその相似比はどうなっているか考え始めると良いでしょう。
■問題
正方形ABCDの辺BCを何等分かし,Bにもっとも近い点をPとします。BからAPに垂直な線をひき,APとの交点をH,AP=10cmとするとき,次の問いに答えなさい。
(1) [図1]のように,辺BCを3等分するとき,BH:HPをもっとも簡単な整数の比で表しなさい。
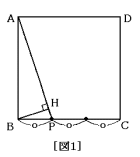
(2) (1) と同様に,辺BCを3等分するとき,正方形ABCDの面積を求めなさい。
(3) BH:HP=7:1のとき,三角形ABPの面積を求めなさい。
(4) 三角形ABHの面積16cm2で三角形BPHの面積が4cm2のとき,正方形ABCDの面積を求めなさい。
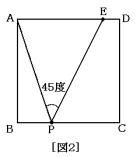
(5) [図2]のように,角APEの大きさが45度になるように点Eをとり,三角形APEの面積が40cm2のとき,BP:PCをもっとも簡単な整数の比で表しなさい。
■解答
直角三角形で直角の頂点から対辺に垂線を引くと,もとの直角三角形と相似な直角三角形が2つできます。
次の図では,三角形ABCと三角形DBAと三角形DACが相似です。
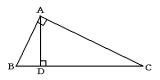
これを使って考えます。
(1) 三角形BHPは三角形ABPと相似です。
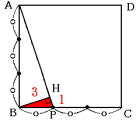
よって,
BH:HP=AB:BP=3:1
答 3:1
(2) 三角形AHBは三角形ABPも相似です。
よって,AH:BH=AB:PB=3:1
(1) の結果も利用し連比を作り考えると,
AH:BH:HP
3: 1
3: 1
───────
9: 3: 1
これより,
AP:BH=(9+1):3=10:3
AP=10cmなので,
BH=10cm×![]() =3cm
=3cm
三角形ABPの面積は,
10cm×3cm÷2=15cm2
正方形ABCDと三角形ABPの面積比は,
(AD+BC):BP=(3+3):1=6:1
正方形ABCDの面積は,
15cm2×6=90cm2
答 90cm2
(3) 三角形BHPと三角形AHBは相似なので,AH:HB(BH)も7:1です。
AH:BH:HP
7: 1
7: 1
───────
49: 7: 1
これから,
AP:BH=(49+1):7=50:7
AP=10cmなので,
BH=10cm×![]() =
=![]() cm
cm
三角形ABPの面積は,
10cm×![]() cm÷2=7cm2
cm÷2=7cm2
答 7cm2
(4) 相似三角形の面積比は相似比の2乗の比になるので,
三角形AHBと三角形BHPの相似比は2:1です。
これから,
AB:BP=2:1
正方形ABCDと三角形ABPの面積比は,
(AD+BC):BP=(2+2):1=4:1
正方形ABCDの面積は,
(16cm2+4cm2)×![]() =80cm2
=80cm2
答 80cm2
(5) 次の図のように,点EからAPに引いた垂線がAPと交わる点をIとすると,
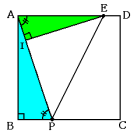
三角形APEで底辺をAPとしたときの高さがEIとなり,その長さは,
40×2÷10=8cm
また,三角形IEPは直角二等辺三角形なので,
EI=PI=8cm
これから,
IA=10−8=2cm
2角が互いに等しいので三角形ABPと三角形EIAは相似です。
よって,
AB:BP=EI:IA=8cm:2cm=4:1
この結果から,
BP:PC=1:(4−1)=1:3
答 1:3