入試問題のポイント（算数）
■点の移動と面積変化のグラフ
同種の問題は私立中でもよく出されますが、図形が単純で計算しやすい点で私立中と 大きく異なります。基本の確認として練習すると良いでしょう。
■問題
次の図１のように，ＡＣの長さは８cm，ＢＣの長さは１０cm，角Ａの大きさは９０
度である直角三角形ＡＢＣがあります。この三角形の辺上を頂点Ａから頂点Ｃを通っ
て頂点Ｂまで，一定の速さで動く点Ｐがあります。
次の図２のグラフは，点Ｐが頂点Ａを出発してからの時間(秒)と三角形ＡＢＰの面
積(ｃm2)の関係を表しています。
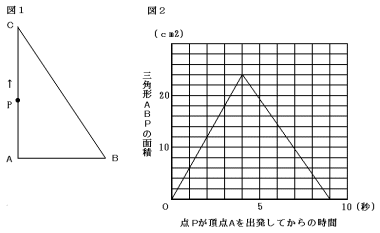
(1) 辺ＡＢの長さは何cmですか。
(2) 点Ｐの速さは毎秒何cmですか。
(3) 点Ｐが頂点Ａを出発して何秒後に，三角形ＡＢＰの面積が１２ｃm2になりますか。
すべて答えなさい。
(4) 直角三角形ＡＢＣの辺上を動く，点Ｐと異なる点Ｑがあります。
点Ｑは，
点Ｐと同じ速さで，頂点Ｂを出発して頂点Ｃを通って頂点Ａまで動きます。
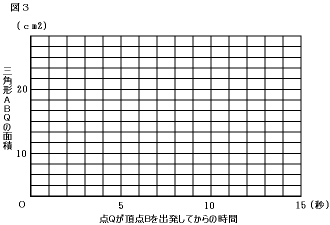
点Ｑが頂点
Ｂを出発してからの時間(秒)と三角形ＡＢＱの面積(ｃm2)の関係を，次の
図３の
グラフにかきなさい。
■解答
(1) 三角形ＡＢＰの面積が三角形ＡＢＣの面積と等しくなるのが４秒後です。
三角形ＡＢＣで底辺をＡＢ，高さをＡＣと考えると，
ＡＢの長さ＝２４ｃm2×２÷８cm＝６cm
別解）３辺の比が３：４：５の三角形は直角三角形です。
この比に当てはまることを利用して，ＡＢ＝６cmと求めた受験生が多かっ
たと思われます。
答 ６cm
(2) 点Ｐは出発後４秒で点Ｃに達したので，
８cm÷４秒＝毎秒２cm
答 毎秒２cm
(3) 次のグラフでわかるように，０〜４秒後の間に１度，４〜９秒の間に１度ありま
す。
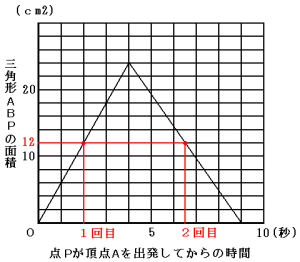
ア）０〜４秒後
面積増加の割合は， ２４ｃm2÷４秒＝毎秒６ｃm2
面積が１２ｃm2の時は， １２ｃm2÷毎秒６ｃm2＝２秒後
イ）４〜９秒後
面積減少の割合は， ２４ｃm2÷５秒＝毎秒
ｃm2
面積が１２ｃm2の時は， ４秒＋１２ｃm2÷毎秒ｃm2＝６
秒後
答 ２秒後，６秒後
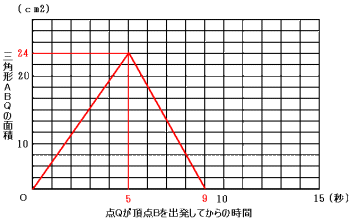
(4) 点Ｑが点Ｃを通過するのは，
１０cm÷毎秒２cm＝５秒後
この時の三角形ＡＢＱの面積は２４ｃm2
点Ｑが点Ａに達するのは，
（１０cm＋８cm）÷毎秒２cm＝９秒後
この時の三角形ＡＢＱの面積は０
これらの値を使ってグラフを描くと，次のようになります。
答