入試問題のポイント（算数）
■線分の長さの比の発展問題
相似や平行線と比例などの線分の長さの比に関する問題はよく出されます。この問題は学力の高い生徒を対象にして作られた問題です。塾によっては「メネラウスの定理」を教える場合もあり，その考え方を用いると計算は楽でしょう。ここでは，一般的な相似の考え方を用いて解きます。
■問題
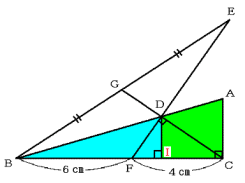
下の図，三角形ＡＢＣは角Ｃが直角の直角三角形です。
点Ｆは辺ＢＣ上にあり，ＢＦ＝６cm，ＦＣ＝４cmです。点Ｆを通る直線と，点Ｃを通る直線が，辺ＡＢ上
の点Ｄで交わるように引き，図のように点ＥとＧを定めたところ，ＤＦ＝ＤＧ，ＢＧ＝ＥＧ，角ＣＤＦ＝９０
度となりました。
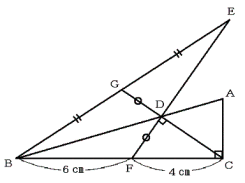
このとき，次の各問いに答えなさい。
(1) ＤＦの長さを求めなさい。
(2) ＡＣの長さを求めなさい。
■解答
(1) 次の図のように辺ＣＧと平行に線分ＦＨを引きます。
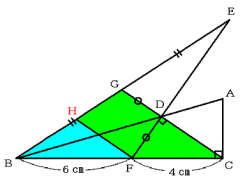
三角形ＢＦＨと三角形ＢＣＧは相似で，その相似比は，
ＢＦ：ＢＣ＝６cm；（６cm＋４cm）＝３：５
よって，
ＦＨ：ＣＧ＝３：５・・・（ア）
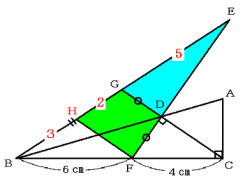
また，三角形ＥＦＨと三角形ＥＤＧも相似です。
平行線と比例の関係から，
ＢＦ：ＦＣ＝ＢＨ：ＨＧ＝２：３
ＢＧ＝ＥＧなので，
ＥＨ：ＥＤ＝（５＋２）：５＝７：５
よって，
ＦＨ：ＤＧ＝７：５・・・（イ）
（ア）（イ）から連比を作ると，
ＦＨ：ＣＧ：ＤＧ
３： ５
７： ５
------------------
２１：３５：１５
これから，ＣＧ：ＤＧ＝３５：１５＝７：３
ここで，ＤＦ：ＤＣ＝ＧＤ：（ＣＧ−ＤＧ）＝３：（７−３）＝３：４
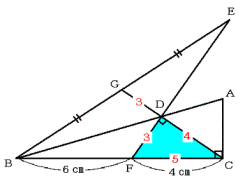
直角を挟む２辺の比が３：４の直角三角形の３辺の比は，３：４：５なので，
ＤＦ＝ＦＣ×
＝４cm×＝２
cm
答 ２cm
(2) 次の図のように点Ｄから辺ＦＣに垂線ＤＩを引きます。
三角形ＣＤＦと三角形ＤＩＦは相似なので，
ＦＩ：ＤＩ：ＤＦ＝３：４：５
ＤＦ＝２cmなので，
ＦＩ＝２cm×＝１
cm
ＤＩ＝２cm×
＝１
cm
三角形ＡＢＣと三角形ＤＢＩは相似で，ＡＣ：ＤＩ＝ＢＣ：ＢＩが成り立ちます。
ＡＣ：１cm＝（６＋４）cm：（６＋１cmより，
ＡＣ＝１×（６＋４）÷（６＋１）
＝２
cm
答 ２cm