入試問題のポイント(算数)
■三角形の辺の長さと面積
三角形を等しい面積に分ける問題です。今までにいろいろな学校で出されてきた問題で、これからも類題が出される可能性があります。線分の長さの比と面積比の問題を考える練習問題や定着を診る確認問題としてもよい問題です。
■問題
下の図のように,直角三角形ABCを直線DE,EF,FG,GH,HBで面積の等しい6個の三角形に分けました。BC=10cm,FD=5cmとして次の問いに答えなさい。
(1) ADの長さを求めなさい。
(2) 三角形ABCの面積を求めなさい。
(3) AE:EG:GBを最も簡単な整数の比で表しなさい。
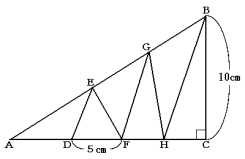
■解答
(1) 高さが等しい三角形の面積比の考え方を利用します。
ACを底辺と考えたときの高さが等しい2つの三角形AEDとDEFの面積が等しいので、
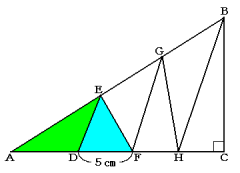
AD=DF
よって、
AD=5cm
答 5cm
(2) 高さが等しい2つの三角形AGFとAGHの面積比が3:4なので、
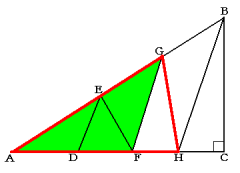
AF:AH=3:4
AF=5cm×2=10cmなので、
AH=10cm×![]() =13
=13![]() cm
cm
同様に2つの三角形ABHとABCの面積比が5:6なので、
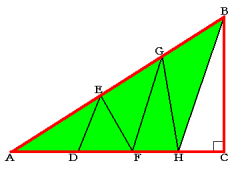
AH:AC=5:6
AC=13![]() cm×
cm×![]() =16cm
=16cm
これから、直角三角形ABCの面積は、
16cm×10cm÷2=80cm2
答 80cm2
(3) ABを底辺と考えた時の高さが等しい2つの三角形に目を着けます。
三角形AEFと三角形EGFの面積比は2:1なので、
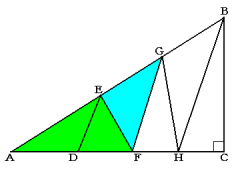
AE:EG=2:1
三角形AGHと三角形GBHの面積比は4:1なので、
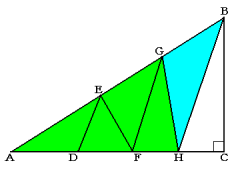
AG:GB=4:1
ここで、AG=4、GB=1とすると、
AE=AG×![]()
=4×![]()
=2![]()
EG=AG×![]()
=4×![]()
=1![]()
よって、
AE:EG:GB=2![]() :1
:1![]() :1
:1
=8:4:3
答 8:4:3