入試問題のポイント(算数)
■物を沈めるときの水の深さの変化
物体を沈めていくとき,押しのけられた水が上に上がり水面が高くなります。そのため,物体が水の中に入っていく速さは,実際に物体が下がっていく速さより大きくなります。このような問題ではその点に注意しながら図に表して解く必要があります。
■問題
下の図のような,水が入った円柱の形の容器があります。この容器の中に底面の円の面積が45cm2,高さが80cmの円柱のおもりを糸につるし,一定の速さでおろしていきます。
また,下のグラフは,おもりが水に入りはじめてから,おもりの底面が容器の底面につくまでの時間と水面までの高さをグラフにしたものです。
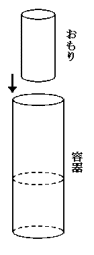
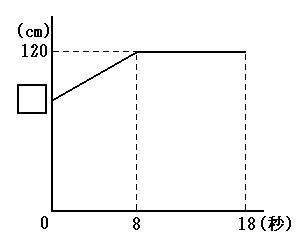
このとき,次の問いに答えなさい。(注意:途中の計算や説明は解答用紙に書きなさい)
(1) おもりのおりる速さは,秒速何cmですか。
(2) グラフの□にあてはまる数を求めなさい。
(3) 容器の底面の面積を求めなさい。
■解答
(1) おもりは完全に水につかってから10秒で底に着いています。
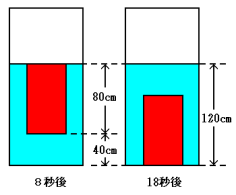
(120cm−80cm)÷(18秒−8秒)
=40cm÷10秒
=毎秒4cm
答 毎秒4cm
(2) □は最初の水面の高さです。
最初の8秒間でおもりが下がった距離は,
毎秒4cm×8秒=32cm
8秒の時点で容器のおもりの底面から容器の底面までの距離は,
毎秒4cm×(18秒−8秒)=40cm
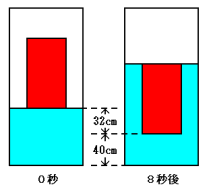
よって,最初の水の深さは,
32cm+40cm=72cm
答 72cm
(3) 水面の高さが120cmになったとき,見かけ上増えた水の体積がおもりの体積です。
おもりの体積は,
45cm2×80cm=3600cm3
見かけ上増えた水の底面積は容器の底面積と等しいので,
3600cm3÷(120cm−72cm)=75cm2
答 75cm2