入試問題のポイント(算数)
■三角形の面積比の問題
相似な三角形や高さが等しい三角形の面積の関係を使って考える問題です。実践女子の問題の中ではかなり難しいものです。しかし,補助線を引いてから基本的な考え方を正確に使うと解けるので,実力をはかるにはよい問題です。
■問題
次の図のような平行四辺形ABCDがあります。この各辺のまん中にそれぞれ点P,Q,R,Sをとり,これらを結ぶと平行四辺形PQRSができます。PSがAQ,ARと交わった点をそれぞれE,FとするとPE:ES=1:2となりました。
次の問いに答えなさい。ただし,答えはすべて最も簡単な整数の比で表しなさい。
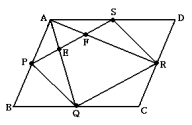
(1) 三角形PBQと三角形QCRの面積の比を求めなさい。
(2) AEとAQの長さの比を求めなさい。
(3) 台形EQRFと平行四辺形ABCDの面積の比を求めなさい。
■解答
(1) 2点P,Rを結びます。
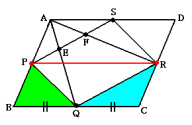
線分PRと辺BCは平行なので,三角形PBQと三角形QCRの高さが等しいことがわかります。
また,BQ=CQから底辺も等しく,三角形PBQと三角形QCRの面積は同じです。
よって,1:1
答 1:1
(2) 2点Q,Sを結びます。
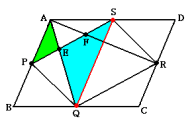
線分SQと辺ABは平行なので,三角形AEPと三角形QESは相似です。
また,AB=QSなので,
AE:QE=AP:QS
=1:2
よって,
AE:AQ=AE:(AE+QE)
=1:3
答 1:3
(3) 相似比が1:3なので,相似な2つの三角形AEFとAQRの面積比は,
(1×1):(3×3)=1:9
三角形AQRは平行四辺形ABCDから3つの三角形ABQ,ADR,CQRを除いて考えることができます。
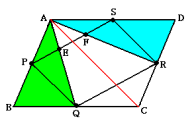
平行四辺形ABCDの面積を1とすると,三角形ABCの面積は![]() です。
です。
三角形ABQ=三角形ABC×![]()
=![]() ×
×![]()
=![]()
三角形ADR=三角形ACD×![]()
=![]() ×
×![]()
=![]()
平行四辺形ABCDの面積を1とすると,三角形BCDの面積も![]() です。
です。
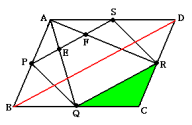
三角形CQR=三角形BCD×![]() ×
×![]()
=![]() ×
×![]() ×
×![]()
=![]()
これらから,
三角形AQR=1−![]() ×2−
×2−![]()
=![]()
台形EQRF=![]() ×
×![]()
=![]()
よって,求める面積比は,
1:![]() =3:1
=3:1
答 3:1