入試問題のポイント(算数)
■容器中の水をこぼす問題
この種の問題はいろいろな学校で出されます。傾けた状態を手前から見た図をもとに考えると解けるものが一般的です。しかし、この問題は水の入っている部分が角柱ではないので、よく考えて解く必要があります。
■問題
次の図のような直角三角形を底面とした三角柱の容器があります。
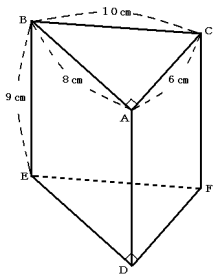
図1のように,この容器のある高さまで水を入れました。そして容器の辺DEを床につけたまま,容器をかたむけました。水がこぼれ始めたのは,図2のときでした。さらに容器をかたむけると,水がこぼれ,図3のようになりました。次の各問いに答えなさい。
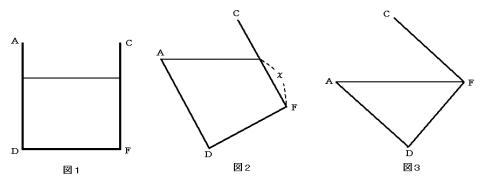
(1) 図3のとき,水が容器に接している部分の面積は何cm2ですか。
(2) 図3のとき,容器に残っている水の体積は何cm3ですか。
(3) 図3のとき,こぼれた水の量は20cm3でした。図2のときのxの長さは何cmですか。
■解答
(1) 水は三角柱の3つの面に接しています。
それらは次の図の三角形ADF、三角形BEF、長方形ABEDにあたります。
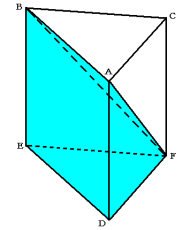
それぞれの面積を求めると、
三角形ADF: 9cm×6cm÷2=27cm2
三角形BEF: 9cm×10cm÷2=45cm2
長方形ABED:9cm×8cm=72cm2
求める面積は、
27cm2+45cm2+72cm2=144cm2
答 144cm2
(2) 上の図のように水が入っている部分を四角錐F−ABEDとして考えます。
この四角錐の体積の高さは辺DFと等しいので、
72cm2×6cm÷3=144cm3
答 144cm3
(3) 水が入っている部分ではなく、水が入っていない部分の体積を使って考えます。
この三角柱の容積は、
(8cm×6cm÷2)×9cm=24cm2×9cm
=216cm3
図2で水が入っていない部分の体積は、
216cm3−(144cm3+20cm3)=52cm3
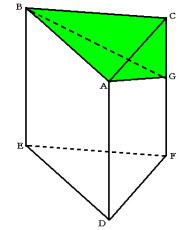
辺CFと水面が交わっている点をGとすると、水が入っていない部分は、底面が三角形ABCで高さ
がCGの三角錐G−ABCと考えることができます。
高さCG:52cm3×3÷24cm2=6![]() cm
cm
求める長さxは、
9cm−6![]() cm=2
cm=2![]() cm
cm
答 2![]() cm
cm