入試問題のポイント（算数）
■相似な三角形の線分比と面積比
相似な三角形を使って長さや面積を求める問題はどの学校でも出されるほどの頻出問題です。ここでは相似比を利用することにこだわり解答を作成しています。
■問題
次の図は辺ＡＢが８cm、辺ＢＣが４cmの長方形と、半径が４cmの半円と四分の一円をあわせたものです。点Ｆを半円の円周の部分の真ん中の点とします。
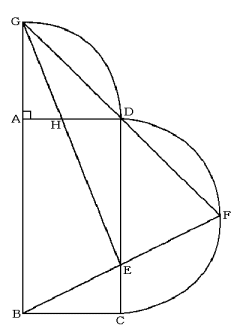
(1) 三角形ＤＥＦの面積＝[ ]ｃm2
(2) 三角形ＤＥＦの面積：三角形ＤＧＨの面積＝[ ]：[ ]
（できるだけ簡単な整数であらわす）
■解答
(1) 三角形ＧＢＦと三角形ＤＥＦは相似です。
点Ｆから辺ＧＡに垂直な直線を引いたとき、辺ＧＢとの交点をＩ、辺ＤＣとの交点をＪとします。
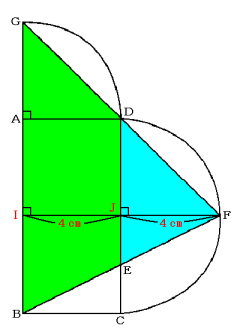
これを利用して、三角形ＧＢＦと三角形ＤＥＦの相似比は、
ＦＩ：ＦＪ＝８cm：４cm
＝２：１
三角形ＧＢＦと三角形ＤＥＦの面積比は、
（２×２）：（１×１）＝４：１
三角形ＧＢＦの面積は、
（４cm＋８cm）×８×
＝４８ｃm2
三角形ＤＥＦの面積は、
４８ｃm2×
＝１２ｃm2
答 １２
(2) 三角形ＧＡＨと三角形ＥＤＨは相似です。
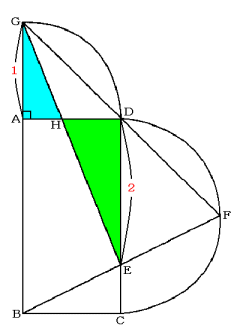
(1) の結果から三角形ＧＢＦと三角形ＤＥＦの相似比は２：１なので、
ＤＥ＝ＧＢ×
＝１２cm×
＝６cm
三角形ＧＡＨと三角形ＥＤＨの相似比は、
ＧＡ：ＥＤ＝４cm：６cm
＝２：３
辺ＨＤの長さは三角形ＤＧＨの底辺にあたります。
その長さは、
４cm×
＝２
cm
三角形ＤＧＨの面積は、
２cm×４cm×＝４
ｃm2
求める面積比は、
１２ｃm2：４ｃm2＝５：２
答 ５、２