入試問題のポイント（算数）
■容器内の水量の変化
容器に水を入れるときの水量（水位）を考える問題は容器の形や入る水の量に変化をつけて、体積の公式を適切に使えるかどうかを診る問題です。この問題では容器から溢れた水の体積も考え合わせて計算する必要があります。
■問題
下図のような直方体の容器Ａ，Ｂ，Ｃがあります。容器Ｂを容器Ｃの中に，容器Ａを容器Ｂの中に入れて固定します。容器Ａに水を入れるとき，容器Ａからあふれた水はすべて容器Ｂに流れ出し，容器Ｃに水を入れるとき，水の高さが容器Ｂの高さをこえると容器Ｂに水が流れこみます。また，容器Ａの（あ）の部分には栓がついていて，栓を開くと，そこから水が毎分２０mlの速さで容器Ｂに流れます。このとき，下の問いに答えなさい。ただし，容器の厚さは考えません。
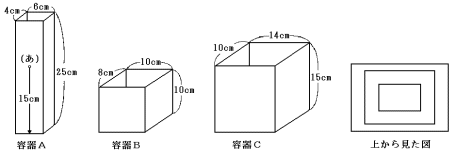
(1) 容器Ａの栓は閉じたまま，容器Ａと容器Ｃにそれぞれ毎分５０mlと毎分７０mlの速さで水を同時に
入れます。容器Ａの水がいっぱいになったとき，容器Ｂには何mlの水が入っていますか。また，容
器Ｂの水がいっばいになるのは水を入れ始めてから何分何秒後ですか。
(2) 容器Ａの栓を開いてから，容器Ａと容器Ｃにそれぞれ毎分５０mlと毎分１００mlの速さで水を同時に
入れます。容器Ａの水がいっぱいになるのは水を入れ始めてから何分何秒後ですか。また，容器
Ｂの水がいっぱいになるのは水を入れ始めてから何分何秒後ですか。
■解答
(1) 容器Ａに水がいっぱいなるまでの時間は、
（４×６×２５）ml÷毎分５０ml＝１２分
この時間までに容器Ｃに入った水の量は、
毎分７０ml×１２分＝８４０ml
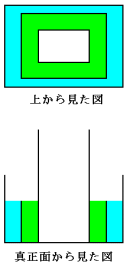
上図で青の部分全体の体積は、
（１０×１４−８×１０）×１０＝６００ml
上図で緑の部分全体の体積は、
（８×１０−４×６）×１０＝５６０ml
よって、緑の部分に１２分後までに入った水の量は、
毎分７０ml×１２分−６００ml＝２４０ml
緑の部分全体の体積より小さいので、この体積が容器Ｂに入った水の体積です。
緑の部分の残りには容器Ａから溢れた水も入ります。
（５６０−２４０）ml÷毎分（７０＋５０）ml＝２
分
容器Ｂに水がいっばいになるまでの時間は、
１２分＋２分＝１４分＝１４分４０秒後
答 ２４０ml、１４分４０秒後
(2) 栓の位置まで水が入るのにかかる時間は、
（４×６×１５）ml÷毎分５０ml＝７
分
その後、いっぱいになるまでの時間は、
｛４×６×（２５−１５）｝ml÷毎分（５０−２０）ml＝８分
よって、容器Ａに水がいっぱいなるまでの時間は、
７分＋８分＝１５分＝１５分１２秒
上図の青の部分にいっぱいになるまでの時間は、
６００ml÷毎分１００ml＝６分
上図の緑の部分には、７分後まで毎分１００mlで入るので、
５６０ml−毎分１００ml×（７−６）分＝４４０ml
残り４４０mlを入れる時は容器Ａの栓から出てくる水が加わります。
４４０ml÷毎分（１００＋２０）ml＝３分
これは８分より短いので次図のように容器Ａから水が溢れる前にいっぱいになります。
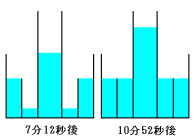
したがって、容器Ｂに水がいっばいになるまでの時間は、
７分＋３分＝１０
分＝１０分５２秒
答 １５分１２秒、１０分５２秒