入試問題のポイント(算数)
■三角形の面積比
この種の問題は中学入試で最もよく出される問題の一つです。「高さが等しい三角形どうしの面積比は底辺の比になる」や「相似な三角形どうしの面積比は対応する辺の長さの比(相似比)の2乗の比になる」などを用いて解くものです。
■問題
次の図で,三角形ABCと三角形EBFは正三角形であり,四角形CDEFは平行四辺形です。三角形EBFと平行四辺形CDEFの面積の比が,1:4のとき,次の問いに答えなさい。ただし,比はもっとも簡単な整数で表しなさい。
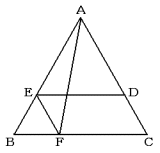
(1) BFとFCの長さの比を求めなさい。
(2) 三角形EBFと三角形AEDの面積の比を求めなさい。
(3) 三角形AEFの面積が8cm2のとき,三角形AEDの面積を求めなさい。
(4) 三角形AEDの面積と三角形DBFの面積が等しくなるように,点Dを辺ACにそって移動させまし
た。このとき,ADとDCの長さの比を求めなさい。
■解答
(1) 平行四辺形CDEFを対角線ECで分けると面積が等しい三角形が2つできます。
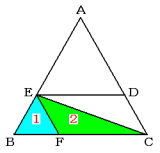
三角形EBFと三角形EFCの面積の比は,
1:(4÷2)=1:2
この2つの三角形は高さが等しいので,面積の比は底辺BFとFCの比と同じです。
よって,BF:FC=1:2
答 1:2
(2) 三角形EBFと三角形AEDはとも正三角形なので,
EB=BF,AE=ED
また,四角形CDEFは平行四辺形なので,
ED=FC
これらから,三角形EBFと三角形AEDの相似比は,
EB:AE=BF:FC
=1:2
よって面積比は,
(1×1):(2×2)=1:4
答 1:4
(3) 三角形AEFと三角形EBFは高さが等しく,底辺の比AE:EBは2:1です。
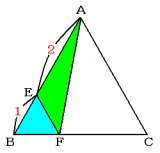
よって,三角形AEFと三角形EBFの面積比も2:1です。
(2) の結果から,三角形EBFと三角形AEDの面積比は,1:4
連比をつくって, 三角形AEF:三角形EBF:三角形AED
2 : 1
1 : 4
----------------------------------------
2 : 1 : 4
三角形AEFと三角形AEDの面積比は,2:4=1:2なので,
8×2=16cm2
答 16cm2
(4) 設問の意味を文字通り「点Dだけが動く」と考えるのがふつうですが,もともとの条件文から「点D
が動くと同時に,点E・Fも動く」と考えることもできます。ともによく出される考え方が使われるの
で両方の解答を示します。
【解答1】
点Dだけが動くと考える場合
次の図のように,三角形AEDの底辺をAEとすると高さはDG,三角形DBFの底辺をBFとすると
高さはDHになります。
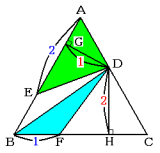
面積が等しい2つの三角形で,底辺の長さの比が2:1なので,高さの比は1:2だとわかります。
三角形DAGと三角形DCHは相似で,相似比はDG:DH=1:2です。
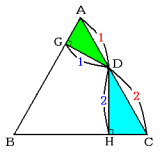
よって,対応する2辺の比DA:DCも1:2です。
答 1:2
【解答2】
点Dが動くと同時に,点E・Fも動くと考える場合
三角形EBFと三角形DBFは底辺が同じで高さも等しいので面積は同じです。
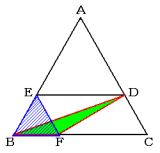
三角形AEDと三角形EBFの面積が等しいと考えます。ともに正三角形なので,合同ならば面積が
等しくなります。
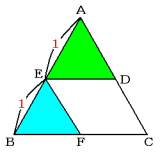
よって,AE:EB=1:1
これから,AD:DC=1:1
答 1:1