入試問題のポイント（算数）
■わり算の応用問題
与えられた指示の通り考えていき，その結果から規則を導く問題は男子難関校で共通して出されているものです。この種の問題は計算をしても単純に答が出せないことが一般的なので，落ち着いて計算し結果の共通点などを見つけることが必要です。
この問題にはいろいろな解法が考えられます。ここでは，２つの数の最大公約数を求める時（特に桁数が多く素因数分解が面倒な時）に使われる「ユークリッドの互除法」を基に作られたものだと考えて，小学校で扱う基本的な考え方だけで解いています。
■問題
太郎君は分数について，次の例に示す方法で余りが０になるまで割り算をしました。
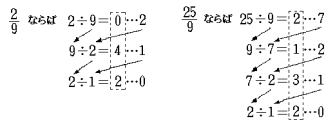
分数について，例のような割り算の商を始めから順番に並べたものを｛Ａ｝とします。
上の例では｛
｝＝（０，４，２），｛
｝＝（２，１，３，２）となります。
(1) 例に示した方法で余りが０になるまで割り算をして｛
｝を求めなさい。ただし，は約分せずに
計算しなさい。
(2) ｛
｝＝（１，３，１，１，３）となりました。整数Ａを求めなさい。
(3) ２つの整数Ｃ，Ｄはたすと２００６となり，｛
｝の始めの部分が（０，１６，…）ととなりました。
｛
｝の始めの部分が（０，ａ，ｂ，…）のとき，ａとｂは
いくつになりますか。理由をつけて答えな
さい。
■解答
(1) 指示通りに計算していきます。
３９÷５４＝０…３９
５４÷３９＝１…１５
３９÷１５＝２… ９
１５÷ ９＝１… ６
９÷ ６＝１… ３
６÷ ３＝２… ０
ここまで終わりです。
よって，（０，１，２，１，１，２）
答 （０，１，２，１，１，２）
＊この計算の結果，あまりが０になる時の３が３９と５４の最大公約数だとわかります。
また，計算途中にでてくる数はすべて最大公約数の倍数になり，最大公約数を元に計算をさか
のぼることができます。
(2) １９２とＡの最大公約数を□として計算を逆から表していきます。数はすべて□の倍数です。
「割られる数＝割る数×商＋あまり」という性質を使い計算をさかのぼっています。
｛｝＝（１，３，１，１，３）なので，
ア÷ □ ＝３…０ から，
ア＝□×３
イ÷（□×３）＝１…□ から，
イ＝（□×３）×１＋□＝□×４
ウ÷（□×４）＝１…（□×３） から，
ウ＝（□×４）×１＋（□×３）＝□×７
Ａ÷（□×７）＝３…（□×４） から，
Ａ＝（□×７）×３＋（□×４）＝□×２５
１９２÷Ａ＝１９２÷（□×２５）
＝１…（□×７） から，
１９２＝（□×２５）×１＋（□×７）＝□×３２
１９２＝□×３２，Ａ＝□×２５ なので，
□＝１９２÷３２＝６
Ａ＝６×２５＝１５０
答 １５０
(3) ｛｝＝（０，１６，…）なので，
Ｃ÷２００６＝０…Ｃ
あまりを△とすると，
２００６÷Ｃ＝１６…△
これから，２００６＝Ｃ×１６＋△なので，
Ｄ＝２００６−Ｃ
＝（Ｃ×１６＋△）−Ｃ
＝Ｃ×１５＋△
また，｛｝＝（０，ａ，ｂ，…）なので，
Ｄ÷２００６＝０…Ｄ
２００６＝Ｃ＋Ｄ，Ｃ＜Ｄなので
２００６÷Ｄ＝（Ｃ＋Ｄ）÷Ｄ＝１…Ｃ
この計算から，ａ＝１
Ｄ＝Ｃ×１５＋△，Ｃ＞△なので，
Ｄ÷Ｃ＝（Ｃ×１５＋△）÷Ｃ＝１５…△
この計算から，ｂ＝１５
答 ａ＝１，ｂ＝１５