入試問題のポイント（算数）
■正六角形の中に作った図形の面積
正六角形が合同な正三角形６つに分けられることを利用する問題です。問題となっている図形がその正三角形のどれだけに相当するかを考えて解くものです。
■問題
正六角形ＡＢＣＤＥＦがあり，図のように点ＰをＡＰの長さがＡＦの
になるように，
点ＱをＣＱの長さがＣＤの
となるようにとります。
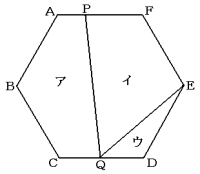
(1) ウの面積は正六角形ＡＢＣＤＥＦの面積の何分のいくつですか。
(2) ア，イ，ウ面積の比を最も簡単な整数の比で表しなさい。
■解答
＊正六角形ＡＢＣＤＥＦの面積を１，もとになる正三角形の面積を
とします。
(1) 次の図で三角形ＱＤＥは，正三角形ＯＣＤと高さが等しく底辺がになっています。
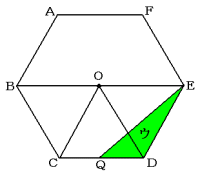
正三角形ＯＣＤはもとになる正三角形なので，
×＝
答
(2) アの部分（五角形ＡＢＣＱＰ）は三角形ＡＢＣと台形ＡＣＱＰに分けられます。
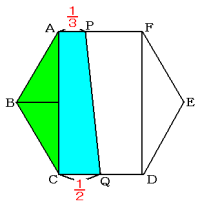
三角形ＡＢＣは基本となる正三角形の半分を２つ集めたものなので，
××２＝
台形ＡＣＱＢは長方形ＡＣＤＦと高さが等しいので，この２つの面積比は，
（＋）：（１＋１）＝
：２＝５：１２
長方形ＡＣＤＦの面積は，
１−×２＝
台形ＡＣＱＢの面積は，長方形ＡＣＤＦの
なので，
×＝
アの部分の面積は，
＋＝
イの部分の面積は，
１−（＋）＝
ア，イ，ウの面積比は，
：：＝１６：１７：３
答 １６：１７：３