入試問題のポイント（算数）
■線分比と面積比
この種の問題はいろいろなかたちで出されます。この問題は補助線を引いて長さを求めるもので，ややレベルが高いと言えます。補助線の引き方は何通りか考えられるので，以下の(2)(3)は１例として紹介します。なおこの問題は「メネラウスの定理」を知っていると，もっとかんたんに計算できます。この定理に興味がある人は塾で教えてもらうとよいでしょう。
■問題
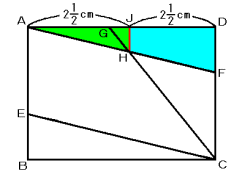
次のような長方形ＡＢＣＤがあります。このとき，次の(1)〜(3)の問いに答えなさい。
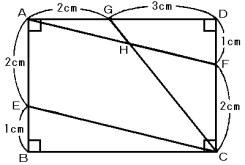
(1) 台形ＡＢＣＦの面積を求めなさい。
(2) 辺の長さの比ＧＨ：ＨＣを求めなさい。
(3) 台形ＡＥＣＨの面積を求めなさい。
■解答
(1) 上底，下底，高さがすべてわかっているので，
（３cm＋２cm）×５cm×
＝１２ｃm2
答 １２ｃm2
(2) 点ＧからＡＦに平行にＧＩを引きます。
三角形ＤＡＦで平行線と比例の関係を使うと，
ＦＩ：ＩＤ＝ＡＧ：ＧＤ＝２：３
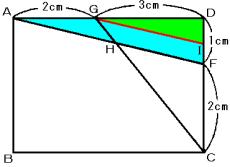
これから，
ＦＩ＝ＦＤ×
＝１cm×
＝cm
三角形ＣＧＩでも平行線と比例の関係を使います。
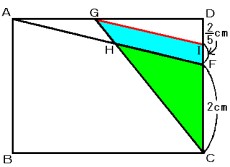
ＣＨ：ＨＧ＝ＣＦ：ＦＩ
＝２cm：cm
＝５：１
答 ５：１
(3) 対辺ＡＥ，ＦＣが平行で長さが等しいので，四角形ＡＥＣＦは平行四辺形です。
平行四辺形ＡＥＣＦと台形ＡＥＣＨの面積比を考えます。
(2) で求めた比を使いたいので，点ＨからＣＤに平行にＨＪを引きます。
三角形ＣＧＤで平行線と比例の関係を使うと，
ＤＪ：ＪＧ＝ＣＨ：ＨＧ＝５：１
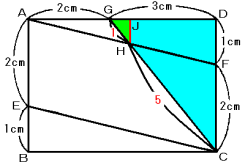
これから，
ＪＧ＝ＤＧ×
＝３cm×
＝cm
三角形ＡＤＦでも平行線と比例の関係を使います。
ＡＨ：ＨＦ＝ＡＪ：ＪＤ
＝（２cm＋cm）：（３cm−cm）
＝２cm：２cm
＝１：１
平行四辺形ＡＥＣＦと台形ＡＥＣＨは高さが等しいので，面積比は，
（ＡＦ＋ＥＣ）：（ＡＨ＋ＥＣ）＝（２＋２）：（１＋２）
＝４：３
平行四辺形ＡＥＣＦの面積は，
２cm×５cm＝１０ｃm2
台形ＡＥＣＨの面積は，
１０ｃm2×
＝７ｃm2
答 ７ｃm2