入試問題のポイント(算数)
■点の移動
速さの問題の応用問題の一つです。ある状態になる時の点の位置を考え,その状態になるまでの時間を考えるのが一般的な問題です。よく出されるので,いろいろなタイプのものを練習しておくとよいでしょう。
■問題
次の図のように,1辺が48cmの正方形ABCDの辺AB,DCの真ん中の点を,それぞれE,Fとします。点Pは点Aを出発して毎秒2cmの速さで辺AD上をくり返し往復します。同様に,点Qは点Fを出発して毎秒3cmの速さで辺FE上を,点Rは点Bを出発して毎秒4cmの速さで辺BC上を,それぞれくり返し往復します。いま,3点P,Q,Rが同時に出発したとして,次の[ ]に適当な数を入れなさい。
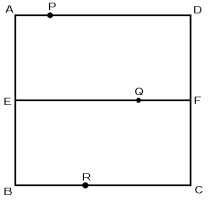
(1) 3点P,Q,Rがはじめてー直線上に並ぶのは,出発してから[ ]秒後です。
(2) はじめて3点P,Q,Rがー直線上に並ぴながら動くのは,出発してから[ア]秒後から[イ]秒後まで
の間です。
■解答
(1) 次の図のように,PRの真ん中の点をSとし,2点Q,Sが重なる時を考えます。
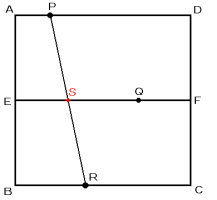
点Sは,点Eを出発後,2点P,Rの平均の速さで進むことになるので,
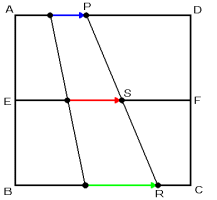
点Sの速さ:(毎秒2cm+毎秒4cm)÷2=毎秒3cm
旅人算の考え方を用いて,
48cm÷(毎秒3cm+毎秒3cm)=8秒
答 8
(2) 条件の通りになるには,2点Q,Sが重なって同じ方向に進む必要があります。
点SはPRの真ん中の点なので,進む方向だけではなく速さも変わります。
なお,3点P,Q,Rの位置関係は周期的に変わるので,3点すべてが同時に最初の位置に戻るま
でを考えるだけでかまいません。
3点それぞれが最初の位置に戻るまでには,
点P:96cm÷毎秒4cm=24秒
点Q:96cm÷毎秒3cm=32秒
点R:96cm÷毎秒2cm=48秒
これらの秒数の最小公倍数96秒後までで考えることにします。
点Sの動く方向は速く動く点Rの動く方向と同じです。
また,速さは点P,Rが同じ向きに進むときには(1) の計算から毎秒3cm
反対向きに進むときには,下の図から考えて,
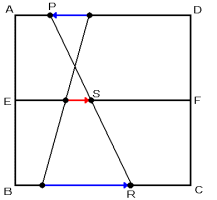
(毎秒4cm−毎秒2cm)÷2=毎秒1cm
以上から点Sの動き方は以下の通りになります。
1.点Rが最初に点Cに着くまで
0〜12秒後で,右向きに毎秒3cm
2.点Pが最初に点Dに着き,同時に点Rが最初に点Bに戻るまで
12〜24秒後で,左向きに毎秒1cm
3.点Rが2度目に点Cに着くまで
24〜36秒後で,右向きに毎秒1cm
4.点Pが最初に点Aに戻り,同時に点Rが2度目に点Bに戻るまで
36〜48秒後で,左向きに毎秒3cm
5.点Rが3度目に点Cに着くまで
48〜60秒後で,右向きに毎秒3cm
6.点Pが2度目に点Dに着き,同時に点Rが3度目に点Bに戻るまで
60〜72秒後で,左向きに毎秒1cm
7.点Rが4度目に点Cに着くまで
72〜84秒後で,右向きに毎秒1cm
8.点Pが2度に点Aに戻り,同時に点Rが4度目に点Bに戻るまで
84〜96秒後で,左向きに毎秒3cm
点Qの動きはそのまま考えて次の通りです。
1.最初に点Eに着くまで
0〜16秒後で,左向きで毎秒3cm
2.最初に点Fに戻るまで
16〜32秒後で,右向きに毎秒3cm
3.2度目に点Eに着くまで
32〜48秒後で,左向きで毎秒3cm
4.2度目に点Fに戻るまで
48〜64秒後で,右向きに毎秒3cm
5.3度目に点Eに着くまで
64〜80秒後で,左向きで毎秒3cm
6.3度目に点Fに戻るまで
80〜96秒後で,右向きに毎秒3cm
2点S,Qで進む方向と速さが同じになるのは2度あるのがわかります。
まず,36〜48秒後で,左向きに毎秒3cm
次に,48〜60秒後で,右向きに毎秒3cm
しかし,この2つは連続した時間なので,答は36〜60秒後です。
答 ア:36 イ:60